About the Odracam Project

The goal is to maximize the beauty, richness, and variety of music. The method is a new music theory based on human cognition, automated by computer. The products are a book explaining the theory, Advanced Music for Beginners (AMFB); and a software suite, Írim, for putting the theory into practice.

The phrase "music theory" may recall to you a dry school subject of limited utility. This does not resemble that. Music causes experiences in the mind. When our theoretical structures mirror those of listeners' experience, we are speaking the ear's language. With good theory, composition is the direct dictation of a musical experience.

The ideas in AMFB are practical and sophisticated, being based on music cognition and a cross-cultural analysis of many traditions. They are automated by a suite of software, Írim, which handles most of the low-level thought and labor (including performance itself). By composing and producing music with the software, you can concentrate on higher-level aspects of the process and create a more beautiful and engaging product.

Here are some highlights (and the gist of them) to give you a taste of what is within:

Flavor Harmony

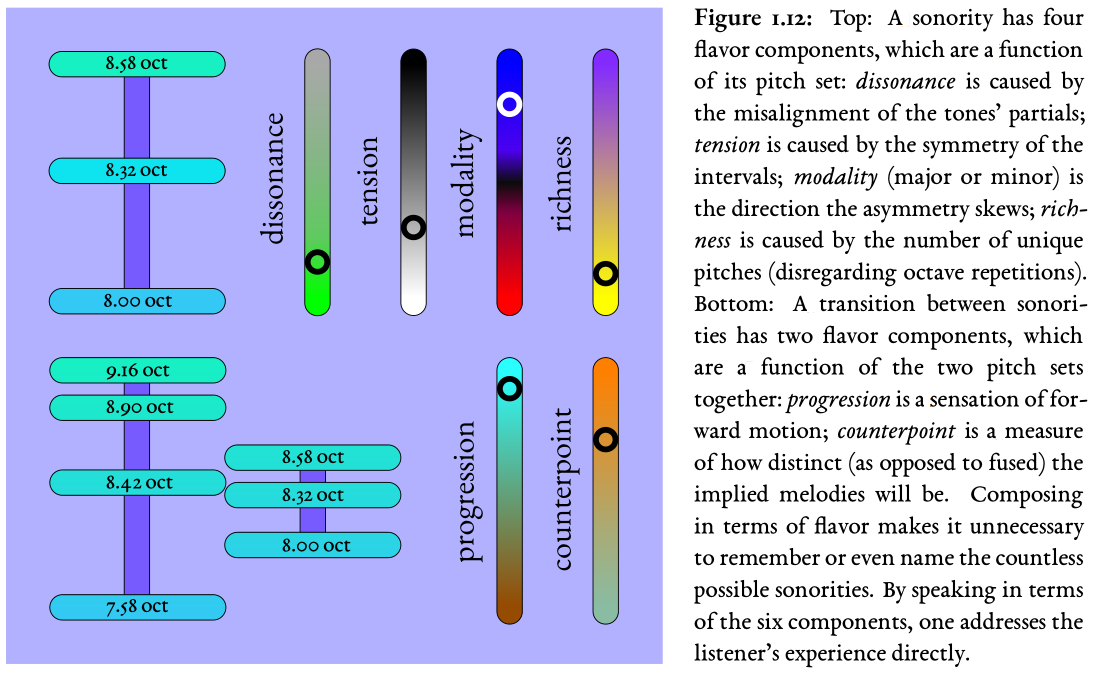
For four centuries, Western musicians have understood harmony as tonal harmony: the idea that chords are locations in an abstract space, so that composers write chord progressions as a travel itinerary which the audience is expected to experience as a journey. This is a captivating idea, but it is deeply flawed.  It requires a lot of training to form the habit of hearing chords in this way. Professionally trained musicians do it, but very few of the audience do—the average audience member is hardly aware of root motion or even of key changes. Everyone, however, including the untrained audience, certainly hears the flavor of sonorities and sonority transitions—these familiar sensations:

1. Dissonance—a physiological unpleasantness produced when the brain knows that there is unresolvable information in a signal.
2. Tension—a savory feeling caused by the symmetry of a sonority (and especially savory when it is relaxed).
3. Modality—the majorness or minorness of a sonority, which depends on the direction its asymmetry skews.
4. Richness—the pleasant complexity that increases with the number of tones in a sonority, and can partially mitigate dissonance.
5. Progression—the feeling that a sonority transition moves the harmony forward. (This is the only flavor that might be culturally-dependent, and it can be re-defined within the system to fit non-Western traditions).
6. Counterpoint—the ease with which the melodic motions (the voice leadings) between two sonorities, can be heard as separate lines, rather than fused together.

Using fuzzy logic, I offer precise mathematical definitions of all of these, so that the flavors can be measured (i.e., a listener's perception of them predicted) for a given sonority or transition.

This suggests two computer programs:

1. The first (HW), given some constraints and parameters, constructs a large database of sonorities and transitions with measured flavors—an harmonic world.
2. The second (HC), given compositional criteria and constraints (including, for example, a melody to be harmonized), finds the sequence of sonorities from the database that most closely matches the criteria.  So, rather than worrying about tonal functions, the composer composes a sequence of flavors—directly painting, in the ear's own terms, the actual experience that the audience will have.

Notice that roots aren't defined and root motion isn't one of the flavors—progression may imply it to some degree, but progression looks at all of the voice leadings in a sonority transition, i.e., the same old tonal pathways are not guaranteed, and non-traditional chords are used without prejudice. The notion of progression introduced here measures the sensation more accurately than root motion, and without introducing the fictional sensation of "root". When looked at in this way, it becomes apparent that root motion was a cumbersome and inaccurate method for suggesting strong progressions, while leaving the other aspects of flavor untheorized, to be learned unconsciously in rote experience.

When flavor harmony is used along with the tuning system described below, one gets perfect harmonic refinement while enjoying complete melodic freedom. It is not even necessary to learn the traditional nomenclature of chords. By automating the low-level decision-making, one can concentrate on high-level aspects of composition.

The Independence of Scale and Tuning

First, I'll show what is wrong with most discourse on tuning, then I'll show how systems of scale and tuning design can be built up rationally and much more usefully—on the basis of human pitch perception.

The most common description of tuning is this: take a "generator" interval, keep adding it to a reference pitch and reducing the result to within an octave until you have enough scalar degrees, i.e., f_i = f₀ (gⁱ mod 2), where f₀ is a reference frequency, scalar degrees are indexed by i={0,N } and, as a first stab, we try g=3/2, N=6. This produces one rigid set of pitches with miserably dissonant thirds. People then think the dissonance problem should be solved with a clever choice of g or by introducing multiple generators to describe a lattice of pitches, and so on. This leads to many puzzles that are delightful to solve but don't serve music well. It's quite possible to waste one's life on mathematical recreations of this kind.

This idea has been with us for 26 centuries, and we learn it in the cradle. Let's examine its assumptions.

1. That a scale's structure (of steps and leaps) must be inseparable from its tuning (the precise intervals between the degrees).
2. That an abstract mathematical procedure must generate the scale-tuning which we then evaluate to see whether we got something desirable: does it have a melodically useful scale structure? Is it consonant?

Admittedly, some of the first assumption follows from the constraint of having only fixed-pitch instruments, but we needn't observe that constraint, especially since we have computers. The second assumption is ridiculous. There is no reason to suppose that (gⁱ mod 2) will yield either good scales or consonant tunings, and generally, it does not. Clever choices of g or other elaborations are not clever at all—the design methodology is flawed. Why not simply decide on the consonant intervals and scale structures we want and use them? If we look carefully at pitch perception, we can see how this is possible.

It's well-known that the ear doesn't care about absolute pitches. It cares about the distance between them—intervals. It's less well-known that there are two kinds of interval perception:  harmonic (between simultaneous tones) and melodic (between consecutive tones). An harmonic interval produces two sensations: dissonance (determined by how the partials of the tones align) and size. Like a moiré pattern, small differences in interval can cause big differences in the alignment of partials, and so big differences in dissonance—this makes our sense of harmonic interval size precise. Melodic intervals also produce the sensation of size but, without the presence of interfering overtones, it is only very approximate.

Melodic intervals lead to a second, more important perception. When listening to a melody the ear quickly and subconsciously forms a model of the underlying pitch collection that it has been drawn from (probably as part of its work in differentiating and tracking separate sound sources). We can represent this sensation (or, as composers, plan it) in the following way:

1. Take an "interval of equivalence", almost always the octave (1200¢).
2. Divide it into N equal bins (12 if you like).
3. These are scalar degrees. Index them by number (or name them C, C♯, D, ... if you wish).
4. When the ear hears a tone in a particular bin, it accepts it as an instance of that degree. For example, if the last tone was an instance of "C" and next is anything in the range 350¢ to 450¢ higher, the ear will take it as an "E".
5. Soon, the ear will have an idea of which bins are used and unused, the "mode" in which the melody plays.

Our theoretical objects should be analogues of listener sensations, and so our "modes"
are objects of this kind—patterns of used and unused bins.

A mode is like the terrain over which the melody moves. Different modes have different affective characters. Modes with the same number of members are interchangeable in the sense that the same melody can easily be played in all of them, taking advantage of their different affects. As composers, we have a lot of choices. In the game of choosing a pattern of M out of N bins, with the conservative range of useful values for N and M something like [5,60] and [5,10], we have vast unexplored melodic territories before us.

Since scales (and their modes) depend on sequential tones, we design them for melodic reasons. Since tunings depend on simultaneous tones, we design them for harmonic reasons. In each context we must observe what the ear considers significant. With melody, the ear wants consistent modes, but available in a variety of modal colors, and the above system maximizes this. When tones are simultaneous, the ear's main desire is consonance, which certain precise intervals can supply.

For example, if we are looking for a "major third" between two consecutive tones, anything around 400¢±50¢ cents will do. (Under laboratory conditions, when we are trying very hard, we can perhaps be more accurate, but in the flow of a musical texture, the ear is not bothering to be.) If, however, we are looking for the same interval between simultaneous tones, we would be best served by a frequency ratio of exactly 5/4, an interval of 386.31¢.

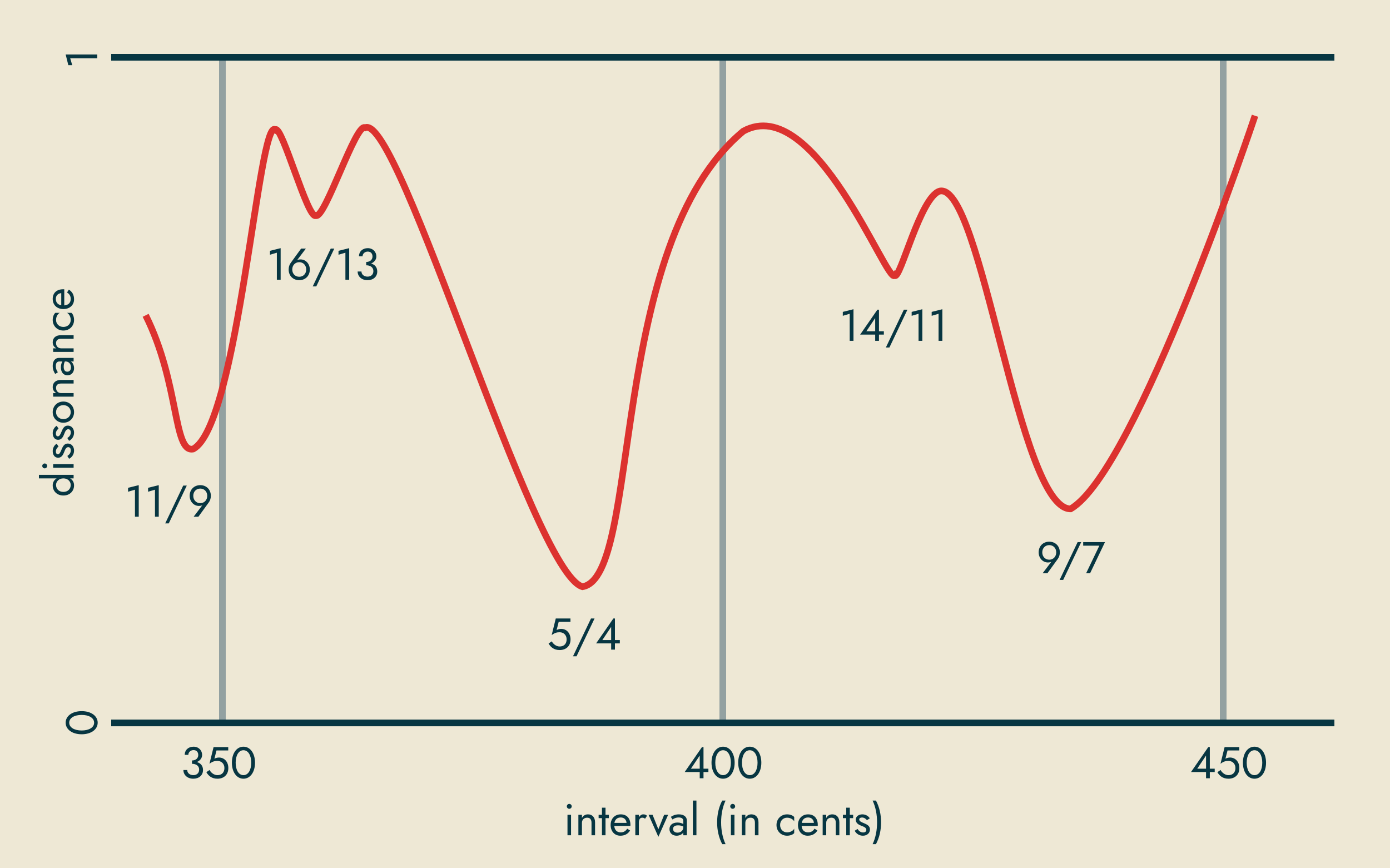
For tones with arbitrary given spectra, we can predict very accurately the dissonance a listener will experience for a given interval. (Most instruments, however, have harmonic spectra, which are least dissonant with frequency ratios of small, whole numbers; I make this assumption here for simplicity.) So, we can plot dissonance as a function of interval.  When we wish to tune the interval between two degrees that we know will be sounding together, we simply seek the minimum of this function in the desired bin range.  The same sort of optimization problem can be solved for any number of simultaneous tones, that is, for any sonority the composer chooses to write.

As an aside, I should point out that there might be several artistically useful local minima in a bin. To extend the above example, 5/4 (386.31¢) is the most consonant interval in the bin, but 9/7 (435¢) is almost as good and 14/11 (418¢) and 16/13 (359¢) might also be useful, because they may belong to sonorities with different flavors. For example, the very same arrangement of bins might allow a pental (using 5/4) or septimal (using 9/7) major triad—the latter is a little more dissonant than the first, but also less tense and more major, which might be preferred in some situations.

I'm not suggesting that composers should do any math, however—adaptive tuning is something for a subroutine to handle. Composers can go on doing what they always do: scheduling the sounding of scalar degrees, i.e., switching bins on and off in time. The computer divides the score into sequential "frames" of time when the set of sounding degrees doesn't change. It then tunes the scale in each frame by this method:

1.  A sonority of N members implies N(N-1)/2 intervals. An optimization routine can find their minimal dissonance together. Often, the intervals involved will be optimal themselves, but often they may require some tempering. E.g., consider a neutral triad: two neutral thirds of about 11/9 (347.4¢) don't quite add up to a perfect fifth of 3/2 (702¢), but taking these values as starting points and fudging each of the three intervals a bit, the computer can find an acceptable triad.
2. The other degrees of the scale (which might be sounding) are then tuned with respect to the pitches of the sonority (which we assume are sounding). The resulting tuned scale is still only relative—we know the intervals between the degrees, but the whole must be placed on the pitch continuum so we can calculate actual frequencies.
3. In the Írim orchestra, the placement is chosen to minimize the sum of the squares of the differences with the previous tuning, so that even a tone held across the boundary will not change noticeably (and one can control the speed and timing of the shift to ensure this). This system allows the pitch standard to drift a little, but because the whole scale is considered and because it's as likely to drift up as down, there is no real danger of drifting away.

Remember, I'm not asking you to do any arithmetic—subroutines perform the calculations and make the choices according to your criteria. As a composer, all you have to do is indicate degrees and times, and there are many tools that can help you to do this, e.g., rhythm and melody generators, as well as the harmony-counterpoint generator mentioned above.

Tuning Paradigms

There are three useful tuning paradigms:

1. Minimal dissonance is generally the best choice,
2. Maximal dissonance is a limited but useful folk practice called Schwebungsdiaphonie, and
3. Controlled dissonance, which can be used for sublime artistic effects.

When using harmonic sounds (as most familiar musical sounds are), minimal dissonance implies just intonation. But, with inharmonic sounds (e.g., chimes and gongs), one might arrive at very different intervals and tunings. Minimal dissonance methods also include techniques for designing timbres to suit arbitrarily tuned scales (as pioneered by William Sethares).

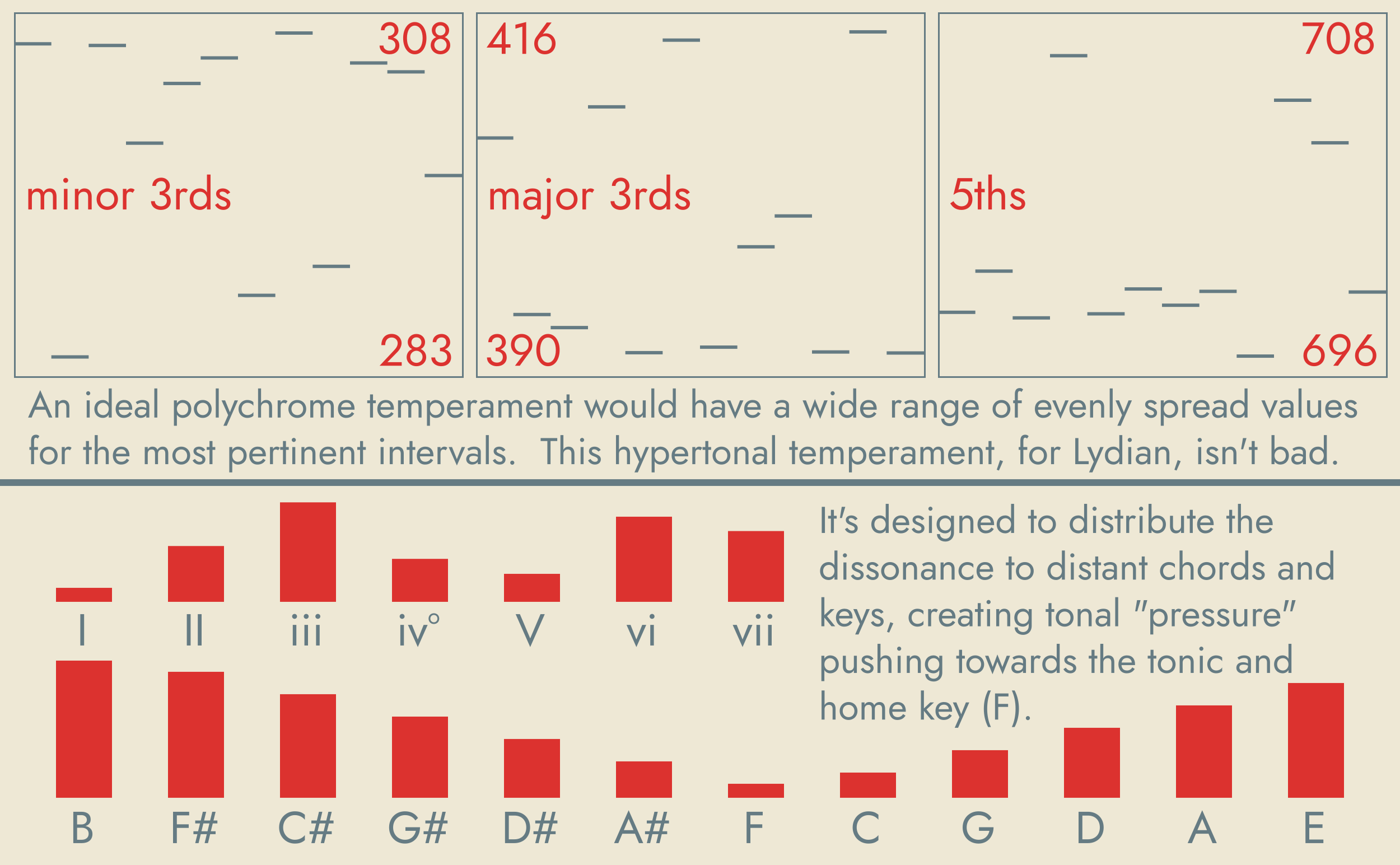
Controlled dissonance is especially well suited to tonal harmony with fixed-pitch instruments. For it, I offer a system for designing well temperaments with two interesting qualities:

1. Polychromaticity—maximally different intervals and therefore chords, and therefore keys, so that every chord and key has its own unique character.
2. Hypertonality—the inevitable dissonance of a fixed scale can be distributed to chords and keys according to their "remoteness", using it to create a natural pressure that pushes the progressions and modulations towards a tonal "home".

Happily, the two are quite compatible.

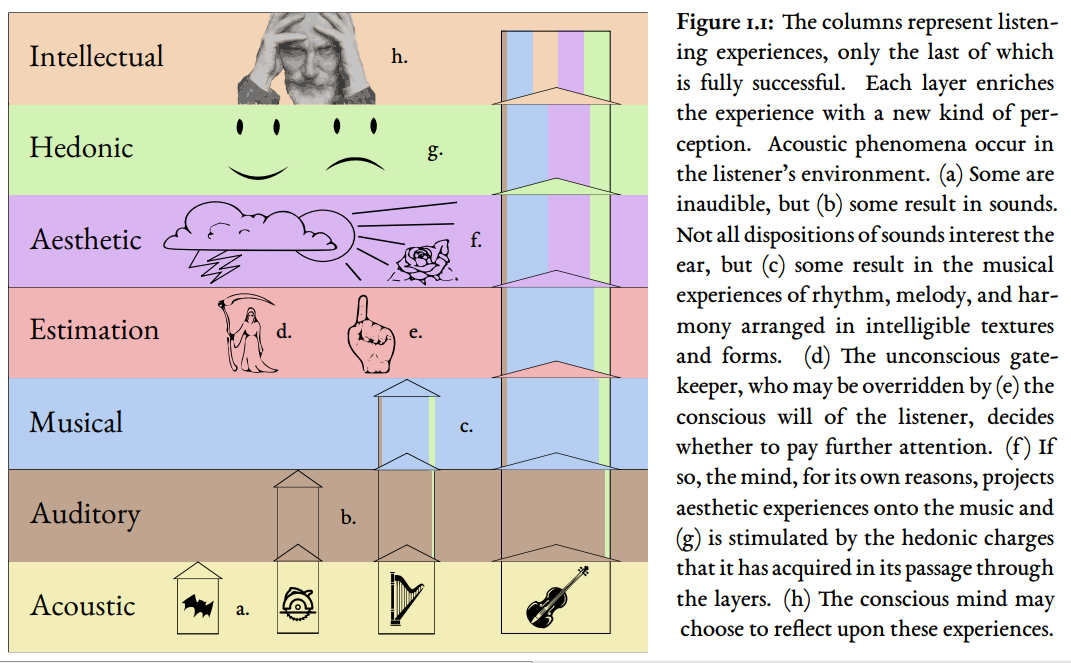
The Seven-Layered Model of Musical Experience

This is a conceptual framework for understanding the listener's experience, so the artist can control it. It describes how mere sounds, auditory sensations of the kind common to all animals, through anomalous neural processing in humans become musical sensations, onto which listeners project aesthetic and other experiences.

For good evolutionary reasons, the ear is very concerned with identifying and locating sound sources in its environment.  This is true for all hearing animals, but in the case of humans, certain patterns of sound can engage neural circuitry that normally has other functions.  For example: certain tone sequences activate the circuits used for speech, causing the sensation we call "melody"—and we pay attention; certain regular patterns of sound engage the circuits used for motion planning, causing the sensation we call "rhythm"—and we feel compelled to move.

For psychological reasons, we project aesthetic sensations like emotion and imagery onto these purely musical sensations.  It is this complex ferment of experiences, charged with their own neurological pleasures and displeasures at every stage, that move us to cogitation and poetry—and we label the whole, "music". 

The seven-layered model explains the relationship of theory to artistry, with important implications for compositional strategy—if we understand how musical experience works, we can find ways to please the audience.

Use Your Imagination:

There are countless ways of composing, but imagine this one to whet your appetite:

1. Suppose you have chosen a meter (say, 2+3) and a mode (based on, say, 6 bins chosen from 11 per octave).
2. You might compose a melody with an automated melody generator—a program which takes into account many factors, including
   a. the rhythm,
   b. a phrase structure,
   c. sections of imitation, and
   d. a melodic mode (of conditional probabilities encapsulated in Markov chains).
3. Imagine the score as a sequence of "frames" to be filled with sonorities. Place your melody in the soprano—on top of the texture. Consider the harmonic rhythm: you want chord transitions once per measure—a structural frame on the first, strong beat—and between these you'll allow a variable number of embellishing frames.
4. Consider the sonority transitions: you insist on good counterpoint throughout, and on strong progression between the structural frames, but you will accept weak progression between the others.
5. Consider the sonority flavors:
   a. Although you prefer minimal dissonance, you are willing to accept more on weak beats and embellishing frames that on strong beats and structural frames.
   b. You indicate a pattern of increasing tension during melodic phrases, dropping sharply near their ends.
   c. Finally, you indicate a preference for high richness and a distribution of 75% minor and 25% major modality.
6. The harmony-counterpoint program (HC) finds the sequence of sonorities that best fits your criteria while harmonizing the given melody. It even writes the embellishing tones for the supporting voices—the little notes that improve the counterpoint and the individual lines. Finally, the texture can be unwoven into a number of simultaneous melodies—the given one which was harmonized, and the supporting parts. The tuning of each sonority was determined for locally maximal consonance (given the pattern of bins and some other factors) back in the HW (harmonic world) program.
7. In performance, the sonorities are lined up on the pitch continuum to minimize drift—whatever the tuning is doing, notes held across frame boundaries suffer minimal change, usually imperceptible and mitigated by unobtrusive "bends". These subtle shifts keep everything exquisitely in tune, just as the best singers do.

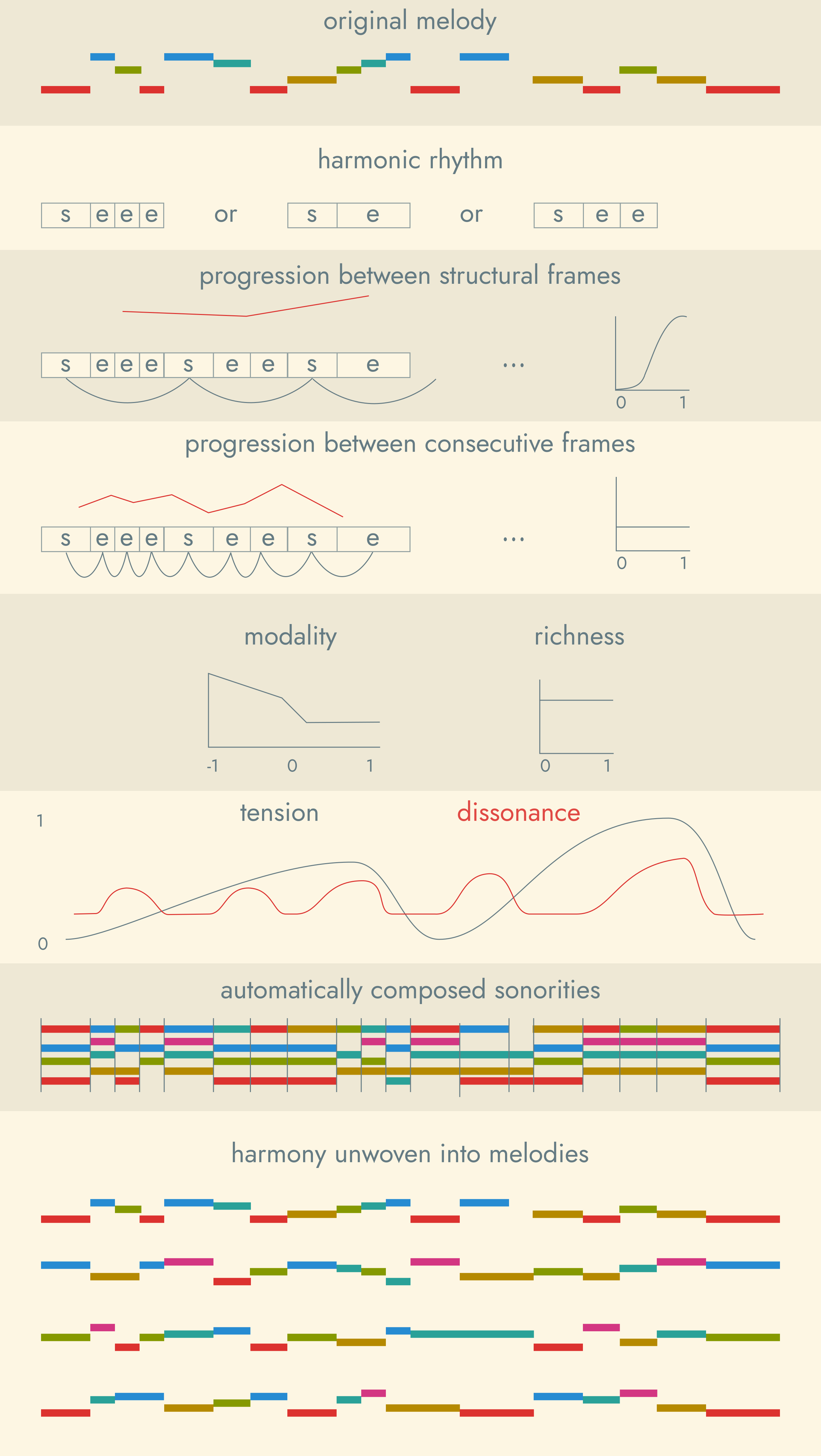
Now, perhaps you especially like one of the supporting lines. You decide to put it in the bass, vary it, and write sonorities above it for the next section, more major this time, and in a different meter and mode...

Welcome to the Website

The Odracam project has two main products:

1. Advanced Music for Beginners, a textbook.
2. Írim, the accompanying software.

It is a work in progress, but already much has been done. In particular, there is a virtual "orchestra" which interprets scores and plays them with human gestures, including adaptive tuning.

You can look under "The Book" to find completed chapters available for download (the Introduction in fasicle 1 contains a detailed outline of the whole project). Under "The Software", you will find the completed software.

"Roadmap" shows the history and plans for the future. There is a forum for discussing the work—and maybe you can lend a hand. There is a page to contact me directly, a blog where I talk about what I'm working on, and a patronage link for support.

Some other cruft has accumulated: other projects of mine, a faq, about the author, and a privacy policy.